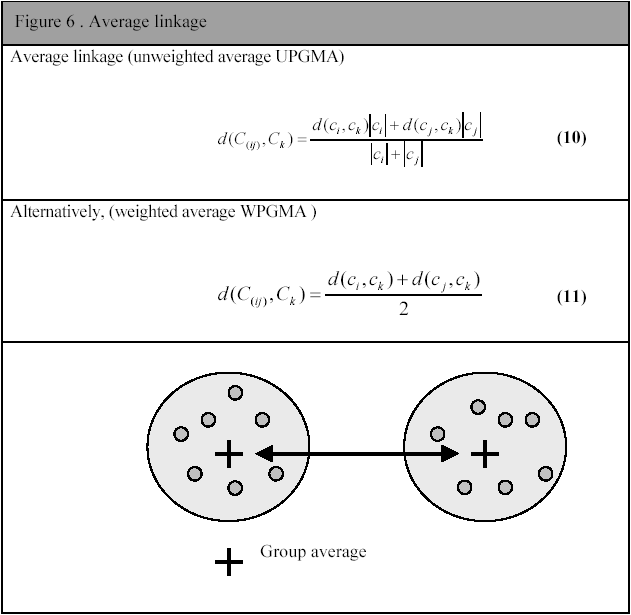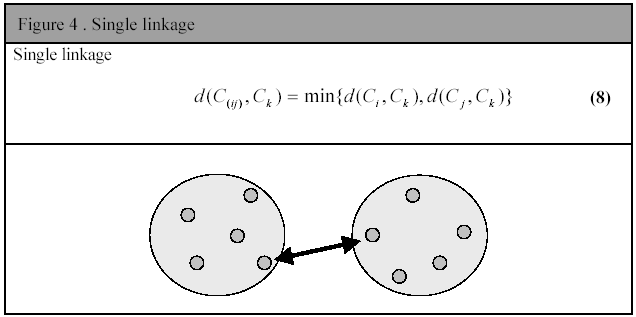
The distance between two objects is defined to be the smallest distance possible between them. If both objects are clusters, the distance between the two closest members are used. This calculation is done by equation (8). Single linkage often produces a very skewed hierarchy (called the chaining problem) and is therefore not very useful for summarizing data. However, outlying objects are easily identified by this method, as they will be the last to be merged.

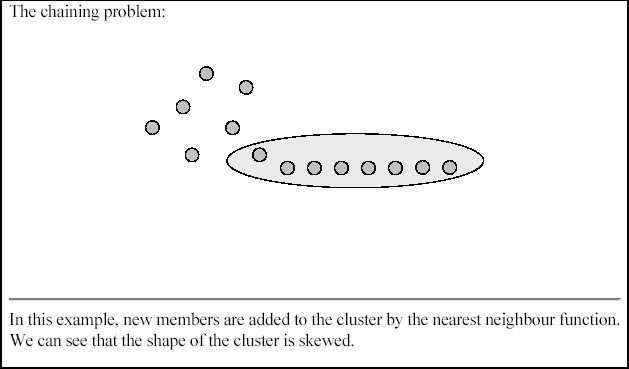
This method is much like the single linkage, but instead of using the minimum of the distances, we use the maximum. Complete linkage tends to be less desirable when there is a considerable amount of noise present in the data. Not surprisingly, complete linkage tends to produce very compact clusters.
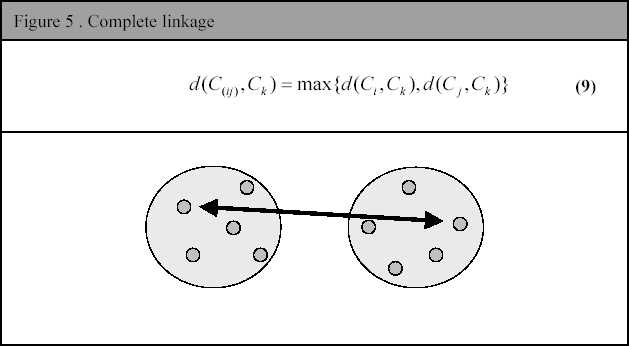
This method takes the mean between all the objects in cluster i to all the objects in cluster j. There are several different ways of defining the average distance. In literature some of these are referred to as WPGMA (weighted pair group method with arithmetic mean), UPGMA (unweighted pair group method with arithmetic mean), UPGMC (unweighted pair group method centroid) and WPGMC (weighted pair group method centroid).